La tesi di Turing-Church è uno dei problemi fondanti dell’informatica per come la conosciamo oggi, e prende ogni presupposto dal trovare una risposta al problema di decisione sollevato da David Hilbert (noto storicamente come entscheidungsproblem, in tedesco, come la lingua parlata dal suo ideatore).
Tale problema si chiede, molto in breve, se si potesse – o meno – stabilire la verità di qualunque enunciato matematico per via di un algoritmo. Il problema di decisione di Hilbert era stato formulato nel 1928 e aveva tenuto banco in ambito accademico per molto tempo.
Nel frattempo (1931) Kurt Gödel aveva dimostrato il teorema di incompletezza, dimostrando che per qualsiasi sistema formale che possa includere l’aritmetica, ci sono proposizioni che sono verità non dimostrabili all’interno di quel sistema. Il teorema di incompletezza ha avuto anch’esso profonde implicazioni per la teoria dei fondamenti della matematica e per la comprensione dei limiti della logica e della dimostrabilità all’interno dei sistemi formali.
Siamo partiti, pertanto, da due aspetti basilari:
- è possibile dimostrare qualsiasi enunciato matematico con un software?
- esistono sistemi formali a base aritmetica che prevedono proposizioni non dimostrabili.
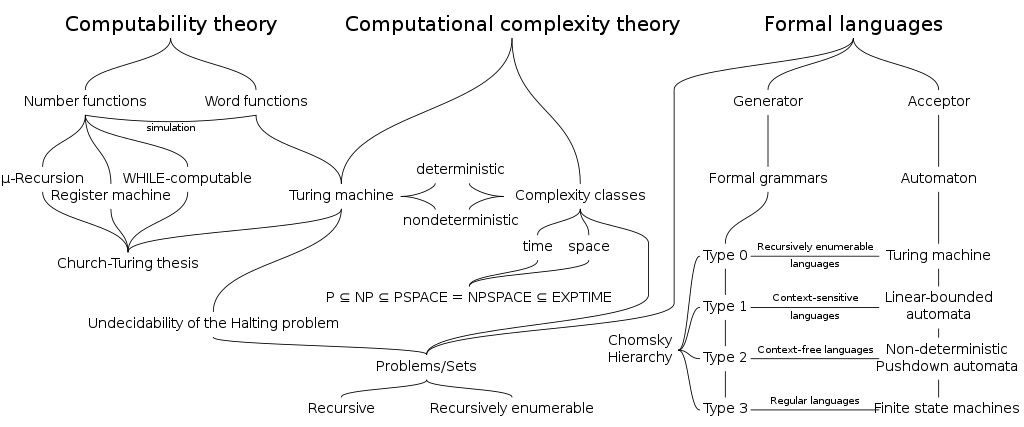
Formulazione della tesi di Church-Turing
la Tesi di Church-Turing afferma che se un certo processo può essere descritto in modo algoritmico (ovvero può essere “calcolato” in senso matematico), allora può essere modellato e simulato da una macchina di Turing. Questo è un principio fondamentale nella teoria dell’informatica che collega diverse nozioni di calcolabilità, come i calcolatori, le funzioni matematiche e i concetti di calcolo.

La Tesi di Church-Turing non è stata dimostrata, ma è piuttosto un’ipotesi che è stata ampiamente accettata sulla base delle prove empiriche che mostrano la capacità delle macchine di Turing e dei modelli equivalenti di esprimere una vasta gamma di processi algoritmici. La tesina ha contribuito a stabilire l’idea di calcolabilità e ha fornito la base per lo sviluppo della teoria dell’informazione e della computazione. Se un linguaggio di programmazione è in grado di esprimere tutte le funzioni calcolabili (cioè, se può simulare il comportamento di una macchina di Turing universale), allora è possibile affermare che quel linguaggio è “computazionalmente completo”.
Questa applicazione aiuta a stabilire i limiti e le capacità di vari linguaggi di programmazione e consente agli sviluppatori di comprendere quali problemi possono essere risolti utilizzando un determinato linguaggio. Ad esempio, la costruzione di linguaggi di programmazione con caratteristiche avanzate o paradigmi specifici può essere guidata dalla comprensione di come tali linguaggi possono simulare le macchine di Turing o altri modelli equivalenti.

Inoltre, la Tesi di Church-Turing è alla base della teoria dell’automazione e dell’informatica teorica. Essa aiuta a definire ciò che può essere calcolato e a stabilire i limiti delle capacità di calcolo. Pertanto, l’applicazione principale della Tesi di Church-Turing è nell’orientare la progettazione dei linguaggi di programmazione, la comprensione della calcolabilità e la definizione dei concetti fondamentali nella teoria dell’informazione e della computazione.