Due figure geometriche si dicono “congruenti” se hanno la stessa forma e le stesse dimensioni, anche se possono essere posizionate in modo diverso nello spazio. In altri termini, pertanto, due figure congruenti sono identiche sotto tutti gli aspetti, come lunghezza dei lati, angoli e aree, ma possono essere orientate in modi diversi. Nella geometria di base, come quella studiata a scuola, la parola congruente è a volte usata come segue.
- Due segmenti sono congruenti se hanno la stessa lunghezza.
- Due angoli sono congruenti se hanno la stessa misura.
- Due cerchi sono congruenti se hanno lo stesso diametro.
In questo senso, due figure piane sono congruenti implica che le loro caratteristiche corrispondenti siano “congruenti” o “uguali” includendo non solo i lati e gli angoli corrispondenti, ma anche le diagonali, i perimetri e le aree corrispondenti.
Dispensa in PDF sulla congruenza tra gli angoli (prof. Angolotti)
Esempio di angoli e figure congruenti
Etimologia e origine del termine – “Congruenti” è un termine che deriva dal latino “congruens”, che significa “che si adatta”, “che corrisponde” o “che è conforme”. In matematica, due figure geometriche si dicono congruenti se hanno le stesse dimensioni e la stessa forma. Più precisamente, due figure geometriche sono congruenti se è possibile sovrapporle in modo che coincidano perfettamente in tutti i loro punti. Questo significa che gli angoli delle due figure devono avere la stessa misura e le lunghezze dei lati devono essere uguali.
Le congruenze sono spesso indicate tramite simboli come il simbolo di congruenza (≅) o mediante descrizioni testuali come “i triangoli ABC e DEF sono congruenti” o “il segmento AB è congruente al segmento CD”.
Le congruenze sono importanti in geometria per identificare figure che sono essenzialmente equivalenti, ma possono apparire in posizioni diverse nello spazio. Questo concetto è fondamentale in molte dimostrazioni geometriche e nella risoluzione di problemi relativi alle figure geometriche.
Ad esempio, due triangoli sono congruenti se hanno tutti e tre i lati rispettivamente congruenti e tutti e tre gli angoli rispettivamente congruenti.
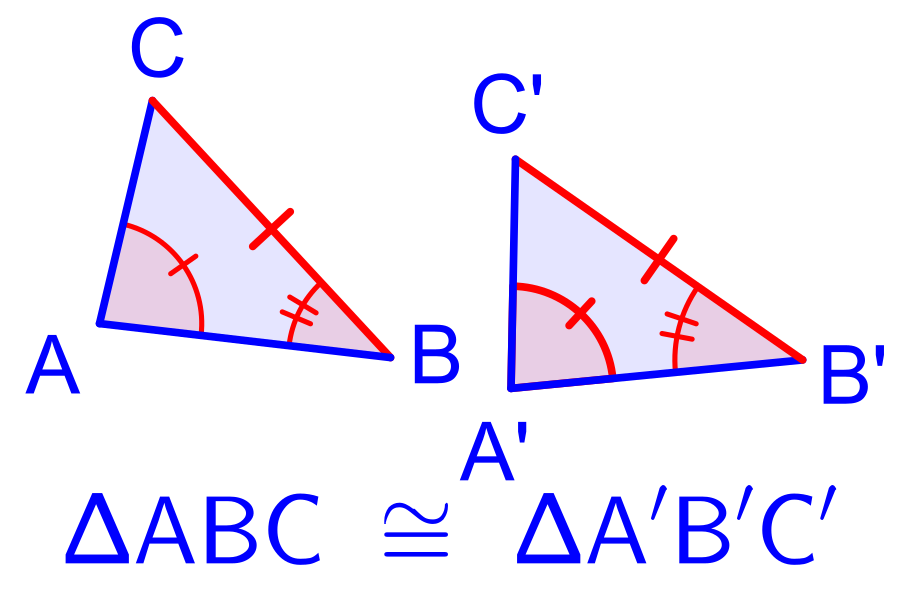
Spiegazione formale
In geometria due figure sono congruenti se hanno la stessa forma e dimensione, oppure se uno ha la stessa forma e dimensione dell’immagine speculare dell’altro. Più formalmente, due insiemi di punti sono detti congruenti se e solo se l’uno può essere trasformato nell’altro mediante un’isometria, ovvero una combinazione di traslazione, rotazione e/o riflessione. Ciò significa che ciascuno degli oggetti può essere riposizionato e riflesso (ma non ridimensionato) in modo da coincidere esattamente con l’altro oggetto. Pertanto due figure piane distinte su un foglio di carta sono congruenti se possono essere ritagliate e poi accostate completamente, con l’eventuale possibilità di girare il foglio.
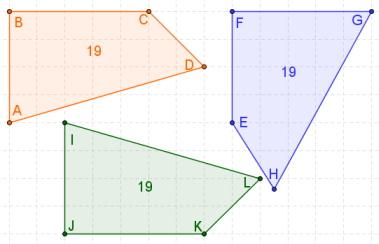
Ad esempio nelle tre figure seguenti quella verde e quella arancione sono tra loro congruenti, al contrario della figura in blu per il fatto che non è sovrapponibile alle altre due.
👇 Contenuti da non perdere 👇
- Domini Internet 🌍
- Informatica 🖥
- Lavoro 🔧
- Meteo
- Programmare 🖥
- Svago 🎈
- 💬 Il nostro canale Telegram: iscriviti
- 🔵 Cosa significa “fan” nel condizionatore
- 🔵 Come indicizzare un sito in WordPress (e non solo)
- 🔵 Strategie di content marketing con le IA
