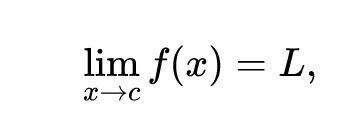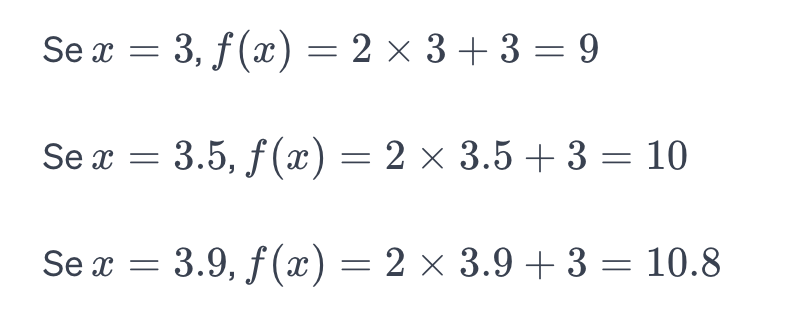In matematica, i limiti sono come delle regole che ci dicono cosa succede quando una cosa si avvicina sempre di più a un certo punto, ma non ci arriva mai del tutto.
Immagina di guardare un punto su una linea, e vuoi vedere cosa succede alla linea quando ti avvicini sempre più a quel punto. Potresti avvicinarti sempre di più, ma potresti non raggiungerlo mai. Il limite ti dice cosa succede alla linea mentre ti avvicini sempre di più a quel punto.
Ad esempio, se hai una funzione matematica che diventa sempre più grande o sempre più piccola mentre ti avvicini a un certo numero, il limite ti dice quale numero diventerà la funzione quando si avvicina il più possibile a quel punto specifico.
I limiti sono importanti perché ci aiutano a capire il comportamento di funzioni matematiche in situazioni in cui non possiamo calcolare direttamente il valore in un certo punto, ma possiamo vedere cosa succede mentre ci avviciniamo sempre di più a quel punto.
In matematica, un limite è il valore verso cui si avvicina una funzione (o una sequenza) mentre l’input (o l’indice) si avvicina a un certo valore. I limiti sono fondamentali per il calcolo differenziale e l’analisi matematica e vengono utilizzati per definire la continuità, le derivate e gli integrali.
Nelle formule, il limite di una funzione di solito viene scritto come lim:
e si legge come ‘il limite di f di x mentre x si avvicina a c è uguale a L‘.
Immaginiamo la funzione
f(x) =
Vogliamo trovare il limite di questa funzione mentre x si avvicina a 4.
Quindi, il limite di f(x) mentre x si avvicina a sarà espresso come limite, per x che tende a 4, di 2x+3:
limx→4(2x+3)
Per calcolare questo limite, sostituiremo gradualmente valori di x sempre più vicini a 4 nella funzione 2x+3:
Continuando così, pertanto, notiamo che quando x si avvicina sempre più a 4, i valori di f(x) si avvicinano a 11. Per intenderci:
Quindi, il limite di f(x) mentre x arriva esattamente a 4 è uguale a 11.
👇 Da non perdere 👇
- 📈 Analizza Cellulari 📱
- 🔐 AI che dolor, Chat 🏴
- 🎯 Targetizza Database SQL 🗄
- 📊 Analizza Errori più comuni 📛
- 🚧 Costruisci Evergreen 📟
- 👩💻 Programma Gratis 🎉
- 💻 Configura Hosting a confronto 💑
- 🔒 Conosci Hosting reti e domini 💻
- 👩💻 Tapioca Informatica 🖥
- 💻 Iconizza Internet 💻
- 🔒 Gestisci Lavoro 🔧
- 💡 Mostra Marketing & SEO 🌪
- 🔑 Apprendi Meteo ⛅
- 🤯 Visiona Mondo Apple 🍎
- 🔍 Supervisiona Mondo Domini 🌐
- 🚀 Metti in cloud monitoraggio servizi online 📈
- 🔮 Anatomizza Nuove tecnologie 🖥
- 🔒 Antani PEC e firma digitale 📩
- 👀 Prematura Programmare 🖥
- 🎮 Lonfa Scrivere 🖋
- 🔒 Conosci Servizi di SMS 📶
- 👀 Guarda Sicurezza informatica e privacy digitale 🖥
- 🎮 Ricorda Siti web 🌎
- 🤖 Ottimizza Spiegoni artificiali 🎓
- 🧠 Neuralizza Svago 🎈
- 📡 Quantizza Usare Excel 🌀
- 🤖 Sovrascrivi Windows 😲
- 🎨 Personalizza Wireless 🚁
- 🔑 Decifra WordPress 🤵
- 💬 Il nostro canale Telegram: iscriviti
- 🟡 Allucinazioni e bias algoritmici. Perchè i software possono “avere le allucinazioni”
- 🟢 Aste di domini, cosa sono e come funzionano
- 🔴 Come scaricare video da TikTok
