0x5f3759df sembra una sequenza di caratteri casuale, senza una logica facile da spiegare, eppure è uno dei numeri più popolari e atipici mai visti in informatica. La sua popolarità – ammettiamo che sia lecito parlare di “popolarità” per un numero! – deriva dall’uso che ne è stato fatto per un particolare algoritmo, che è quello del calcolo della radice quadrata inversa.
Radice quadrata inversa
Una radice quadrata inversa è semplicemente 1 fratto radice di x, ovvero:
Radice quadrata inversa veloce
La radice quadrata inversa veloce (Fast InvSqrt() o mediante numero esadecimale 0x5F3759DF), è un algoritmo che stima il reciproco o inverso di una radice quadrata che abbiamo appena visto, dove x è un numero in virgola mobile a 32 bit, sfruttando il formato internazionale detto IEEE 754.
In questo standard sfruttiamo il primo bit per il segno (0 se numero positivo, 1 se numero negativo), gli altri 8 per l’esponente e i restanti 23 per la mantissa, il che rappresenta qualsiasi numero decimale con segno mediante l’espressione matematica:
1 8 23 lunghezza in bit +-+--------+-----------------------+ |S| Esp. | Mantissa | +-+--------+-----------------------+ 31 30 22 0 indice dei bit
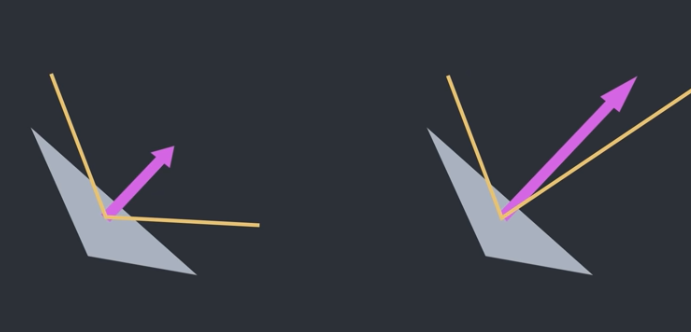
In genere i software di grafica tridimensionale utilizzano le radici quadrate inverse per calcolare gli angoli di incidenza e riflessione per l’illuminazione e le ombre. Se non calcolati correttamente, incidono molto negativamente sulla resa grafica del giorno, rendendolo irrealistico o qualitativamente scarso. Se il calcolo delle radici quadrate inverse “pesa” computazionalmente in termini di numerose divisioni tra numeri decimali, l’algoritmo del quadrato inverso veloce è in grado di generare una buona approssimazione con una singola divisione. Prima dei primi anni 2000, l’algoritmo non era noto pubblicamente, per poi diventare uno dei più citati e istruttivi mai realizzati in informatica.
Per capire meglio i come ed i perchè di questa storia, è bene fare un piccolo passo indietro e contestualizzare.
CPU e approssimazione di numeri
Il computer è uno strumento di calcolo e, per come funziona ed ha funzionato fin dalla sua nascita, lavora sui bit: enormi sequenze di zero e di uno che sono trattate al ritmo scandito dalla frequenza della CPU. Tutto è numero, per un computer, e per avere massima efficenza di calcolo e prestazioni è bene che i calcoli anche se complessi siano sempre corretti o molto ben approssimati. Altrettanto chiaro che, dato il contesto, è preferibile che si lavori sempre con cifre esatte, intere, cosa non sempre possibile, e che i calcoli non siano “costretti” a dover gestire numeri decimali: questo perchè tali numeri sono approssimati, e nel caso dei numeri irrazionali (teoricamente infiniti) costringono di fatto il processore ed i registri del computer a “tagliare” la cifra stessa, con l’introduzione di errori di approssimazione all’interno della parte decimale stessa.
Da Pitagora a Quake III: perchè 0x5f3759df è così interessante?
Chiedersi cosa c’entri tutto questo con il numero esadecimale 0x5f3759df significa essere molto curiosi, senza dubbio, ma anche porsi il problema del calcolo della radice quadrata inversa. La popolarità del numero in formato esadecimale 0x5f3759df nasce, quantomeno tra gli informatici, con la pubblicazione in formato open source (sorgente aperto, codice ispezionabile da chiunque) del codice del videogame Quake III.
Del resto già i pitagorici si erano accorti, tra il 570 e il 490 a.C, che basta un triangolo rettangolo di lato 1 per ottenere un ipotenusa pari a √2 (radice quadrata di due), un numero irrazionale che un computer avrebbe seri problemi a trattare. La cosa li aveva mandati in crisi, perchè quel valore calcolato approssimativamente sembrava disconfermare l’idea che “tutto è numero“, senza contare che per un computer non può esistere una rappresentazione illimitata. Ma allora, uno potrebbe chiedersi, tutto è numero o no? In natura forse, nel mondo dei computer è vero “fino ad un certo punto”.
Vale la pena di rendersi conto del problema in fase preliminare, per poi capirlo meglio nel contesto di cui parliamo. Per un computer, radice quadrata di 2, nello specifco, è un numero irrazionale ed avrà sempre una lunghezza finita:
1.41421
ad esempio, quando in realtà la matematica stabilisce essere una cifra infinitamente più lunga.
Nota. 5f3759df espresso come numero decimale equivale a: 5∙167+15∙166+3∙165+7∙164+5∙163+9∙162+13∙161+15∙160 = 5∙268435456+15∙16777216+3∙1048576+7∙65536+5∙4096+9∙256+13∙16+15∙1 = 1342177280+251658240+3145728+458752+20480+2304+208+15 =
159746300710
Quando si è lavorato alla grafica 3D di Quake II, nello specifico, si è posto il problema di effettuare il calcolo di una proiezione ortogonale in uno spazio a 3 dimensioni. La normalizzazione di ogni vettore nello spazio, in altri termini, implica che io debba esprimere in base uno ognuno di essi, pena una autentica distorsione spaziale e mancata proporzione del personaggio, degli ambienti e/o degli oggetti presenti nel gioco.
Rappresentazione di uno spazio 3D in un videogame
Se immaginiamo un videogioco con 4 personaggi, 1 stanza e 5 oggetti al suo interno, dovrò effettuare questa normalizzazione per 1+4+5 = 10 volte x 3 dimensioni = 30 volte in tutto, ad una velocità pari alla frequenza di aggiornamento dell’animazione del gioco, che è dell’ordine dei microsecondi e/o millisecondi (calcolo semplificato, ma serve giusto a capire che sono calcoli molto, molto frequenti).
Estendendo il teorema di Pitagora (c’è sempre lui di mezzo, in effetti) da due dimensioni (l’ipotenusa è pari alla radice dei quadrati dei due cateti):
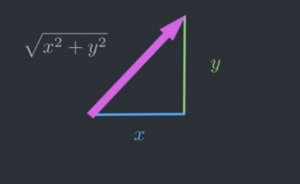
fino a tre dimensioni:
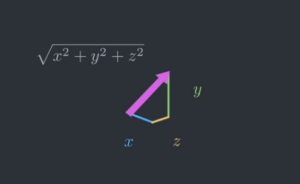
non dovrebbe essere difficile convincersi che per normalizzare i tre vettori x (larghezza), y (altezza), z (profondità), non dobbiamo fare altro se non dividere la dimensione in pixel di ognuno di essi per la radice della somma dei tre quadrati, il che (ad esempio su z) equivale a moltiplicare per l’inverso di una radice quadrata (ci siamo arrivati: ecco a cosa serve! Se non fosse chiaro: la radice quadrata inversa serve a normalizzare i tre vettori x, y, z per ottenere uno spazio in tre dimensioni equilibrato, uniforme e realistico)
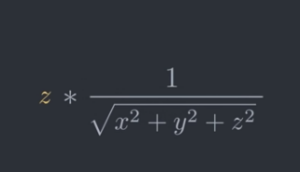
Il problema adesso è il seguente: se le somme sono operazioni che un computer può fare velocemente, e la stessa cosa vale per i quadrati (che sono prodotti: x al quadrato per un computer diventa x * x, ad esempio), non pssiamo dire lo stesso per frazione e radice quadrata, che ad una CPU costano molte operazioni.
La soluzione da sfruttare
La soluzione è quella, poco ovvia dal nostro punto di vista ma parecchio tale per un computer, quella di trattare con variabili che siano bitwise, ovvero sulle quali io possa operare bit a bit, il che è più veloce, ovvero: shift a destra e sinistra, inversione di bit, ecc.
Stiamo per arrivare al punto per cui, di fatto, con un po’ di pazienza capiremo come si calcola una radice inversa approssimata. In C++, il calcolo di una radice quadrata inversa “ordinaria” equivale a:
x_norm = 1 / sqrt(x*x + y*y + z*)
il che è pero’ computazionalmente pesante, per quanto abbiamo visto. Specie per l’hardware dell’epoca, non potevano permettersi una simile inefficenza.

Uso della radice quadrata inversa in Quake III
Questo è il frammento di codice originale che si occupa della radice quadrata inversa:
In breve. L’algoritmo accetta un numero in virgola mobile a 32 bit come input, poi memorizza un valore dimezzato per un uso successivo. A questo punto, trattando i bit che rappresentano il numero in virgola mobile come un numero intero a 32 bit, viene eseguito uno shift a destra di un bit (che equivale ad una divisione del numero per 2) e il risultato viene sottratto dal numero 0x5F3759DF (in notazione decimale è 1.597.463.007), che è una rappresentazione in virgola mobile del numero che risulta da calcoli matematici, ovvero
(radice quadrata di 2 alla 127). Ciò si tradurrà in una prima approssimazione della radice quadrata inversa dell’input, in base ad un procedimento matematico esplicato nel dettaglio qui. Trattando i bit come un numero in virgola mobile, viene in seguito applicata una singola iterazione del metodo delle tangenti, ottenendo un’approssimazione ancora più precisa. L’algoritmo termina e restituisce un’approssimazione dell’inverso della radice quadrata desiderata.
In C++ si scrive generalmente così.
float Q_rsqrt( float number ) { long i; float x2, y; const float threehalfs = 1.5F; x2 = number * 0.5F; y = number; i = * ( long * ) &y; // evil floating point bit level hacking i = 0x5f3759df - ( i >> 1 ); // what the fuck? y = * ( float * ) &i; y = y * ( threehalfs - ( x2 * y * y ) ); // 1st iteration // y = y * ( threehalfs - ( x2 * y * y ) ); // 2nd iteration, this can be removed return y; }
Andiamo a vedere cosa succede riga per riga; number è, per inciso, il numero di cui vogliamo calcolare la radice inversa (la coordinata x, y o z).
long i;
rappresenta un numero intero di tipo long, in cui sono presenti 4 ottetti (4 byte). Considerevolmente, i long si prestano ad operazioni bit a bit (dette a volte bitwise), il che ci aiuterà per quello che vogliamo fare.
float x2, y;
rappresenta due numeri decimali di tipo float, in cui sono presenti 4 byte. La notazione è la IEEE 754, cosa utile per consentire la correttezza dei calcoli successivi, anche se qui il bitwise non è supportato.
const float threehalfs = 1.5F;
Esiste a questo punto la costante threehalfs (3 mezzi, letteralmente), che poniamo pari a 1.5 per comodità.
x2 = number * 0.5F; y = number;
il che, a ben vedere, è un modo rapido per consentire la divisione di number per 2, moltiplicandolo per 0.5 (equivalente, a meno di eventuali approssimazioni di calcolo). Nella seconda riga, poi, molto semplicemente si va ad assegnare a y il valore del numero calcolato (sempre due float sono, del resto).
Adesso viene il bello – o, se preferite, la parte più difficile del calcolo:
i = * ( long * ) &y;
l’algoritmo in questa fase memorizza dentro i il valore dello shift sugli indirizzi di memoria delle variabili: prima su &y, poi su long*, poi di nuovo sul risultato (* iniziale). L’operazione è veloce anche perchè avviene sugli indirizzi di memoria e non sul contenuto delle variabili. Vale la pena di osservare, a questo punto, che se devo calcolare una radice quadrata, posso scriverla matematicamente secondo la seguente equivalenza:

ovvero: l’inverso di una radice quadrata di x si può scrivere come x elevato a -1/2. In termini di bit, dividere per due in linguaggio C++ significa shiftare i bit di x (che abbiamo conservato mediante long dentro i, lo ricordiamo tanto per non perdere il filo del discorso) a destra.
i = 0x5f3759df - ( i >> 1 ); // what the fuck?
il che equivale a sottrarre dal numero magico 0x5f3759df il valore di i shiftato a destra (diviso per 2).
y = * ( float * ) &i;
In questo passaggio prendiamo l’indirizzo di memoria di i, e lo convertiamo in float mediante puntatore.
y = y * ( threehalfs - ( x2 * y * y ) ); // 1st iteration
Applichiamo qui il metodo di Newton e, a questo punto, il calcolo è stato effettuato in una singola iterazione.
// y = y * ( threehalfs - ( x2 * y * y ) ); // 2nd iteration, this can be removed return y;
Test sul campo in C++ della radice quadrata inversa
Per vedere il risultato nella pratica, proviamo a vedere la differenza tra calcolo tradizionale e calcolo approssimato. Usiamo questo codice (disponibile su Github qui):
#include <iostream>
#include <math.h>
using namespace std;
float Q_rsqrt( float number )
{
long i;
float x2, y;
const float threehalfs = 1.5F;
x2 = number * 0.5F;
y = number;
i = * ( long * ) &y; // evil floating point bit level hacking
i = 0x5f3759df - ( i >> 1 ); // what the fuck?
y = * ( float * ) &i;
y = y * ( threehalfs - ( x2 * y * y ) ); // 1st iteration
// y = y * ( threehalfs - ( x2 * y * y ) ); // 2nd iteration, this can be removed
return y;
}
int main()
{
int x = 34;
float y = 1 / sqrt(x);
float y1 = Q_rsqrt(x);
cout << "La radice inversa esatta di "<<x<<" è: "<<y;
cout << "\n La radice inversa approssimata di "<<x<<" è: "<<y1;
return 0;
}
che darà come risultato:
La radice inversa esatta di 34 è: 0.171499 La radice inversa approssimata di 34 è: 0.171381
...Program finished with exit code 0
Sono due risultati che coincidono in modo approssimato, per quanto il calcolo sia identico fino alla terza cifra decimale.
A cosa serve nella grafica 3D la radice quadrata inversa?
Alla lunga, l’uso della radice inversa approssimata paga in termini di prestazioni: se dobbiamo eseguire molte radici inverse ogni secondo, come avviene per le animazioni 3D che ragionano a 25 FPS (tanto per avere una misura orientativa), ciò coinciderà con 25 x 3 = 75 calcoli per ogni singolo oggetto in 3D che si sta muovendo nella scena.
Nel seguente video di esempio, viene mostrata la differenza di rendering tra un metodo di calcolo e l’altro.
Foto di copertina di Kevin Ku.
👇 Da non perdere 👇
- 📈 Analizza Cellulari 📱
- 🔐 AI che dolor, Chat 🏴
- 🎯 Targetizza Database SQL 🗄
- 📊 Analizza Errori più comuni 📛
- 🚧 Costruisci Evergreen 📟
- 👩💻 Programma Gratis 🎉
- 💻 Configura Hosting a confronto 💑
- 🔒 Conosci Hosting reti e domini 💻
- 👩💻 Tapioca Informatica 🖥
- 💻 Iconizza Internet 💻
- 🔒 Gestisci Lavoro 🔧
- 💡 Mostra Marketing & SEO 🌪
- 🔑 Apprendi Meteo ⛅
- 🤯 Visiona Mondo Apple 🍎
- 🔍 Supervisiona Mondo Domini 🌐
- 🚀 Metti in cloud monitoraggio servizi online 📈
- 🔮 Anatomizza Nuove tecnologie 🖥
- 🔒 Antani PEC e firma digitale 📩
- 👀 Prematura Programmare 🖥
- 🎮 Lonfa Scrivere 🖋
- 🔒 Conosci Servizi di SMS 📶
- 👀 Guarda Sicurezza informatica e privacy digitale 🖥
- 🎮 Ricorda Siti web 🌎
- 🤖 Ottimizza Spiegoni artificiali 🎓
- 🧠 Neuralizza Svago 🎈
- 📡 Quantizza Usare Excel 🌀
- 🤖 Sovrascrivi Windows 😲
- 🎨 Personalizza Wireless 🚁
- 🔑 Decifra WordPress 🤵
- 💬 Il nostro canale Telegram: iscriviti
- 🟠 Il tuo pacco sta arrivando – ma è solo una truffa
- 🟠 Requisiti Joomla!: come e dove farlo funzionare
- 🟡 Il tuo pacco sta arrivando – ma è solo una truffa