PRT96919
La tesi di Turing-Church parte dal presupposto di risolvere il problema di decisione sollevato dal matematico Hilbert (Entscheidungsproblem), che stabilisce se si possa o meno decidere la verità di qualunque enunciato matematico per via di un algoritmo. Il problema di decisione di Hilbert è un importante problema formulato nel 1928 che ha tenuto banco in ambito accademico per molto tempo.
Esso chiede se esista o meno un algoritmo che, dato un enunciato matematico qualsiasi, possa stabilire in maniera finita se quell’enunciato è dimostrabile all’interno di un sistema formale dato. Il problema si riferisce specificamente all’insieme delle proposizioni dimostrabili, senza considerare se l’enunciato sia effettivamente vero nel contesto della matematica. Nel 1931, infatti, Kurt Gödel dimostrò il suo famoso teorema di incompletezza, dimostrando che per qualsiasi sistema formale abbastanza potente da includere l’aritmetica, ci sono proposizioni che sono verità indimostrabili all’interno di quel sistema. Questo teorema di incompletezza di Gödel ha avuto profonde implicazioni per la teoria dei fondamenti della matematica e per la comprensione dei limiti della logica e della dimostrabilità all’interno dei sistemi formali.
PRT96919
Uno schema riassuntivo di informatica teorica e dei suoi concetti base. RobinK, Paeng, Mkleine, CC BY-SA 3.0 <http://creativecommons.org/licenses/by-sa/3.0/>, via Wikimedia Commons
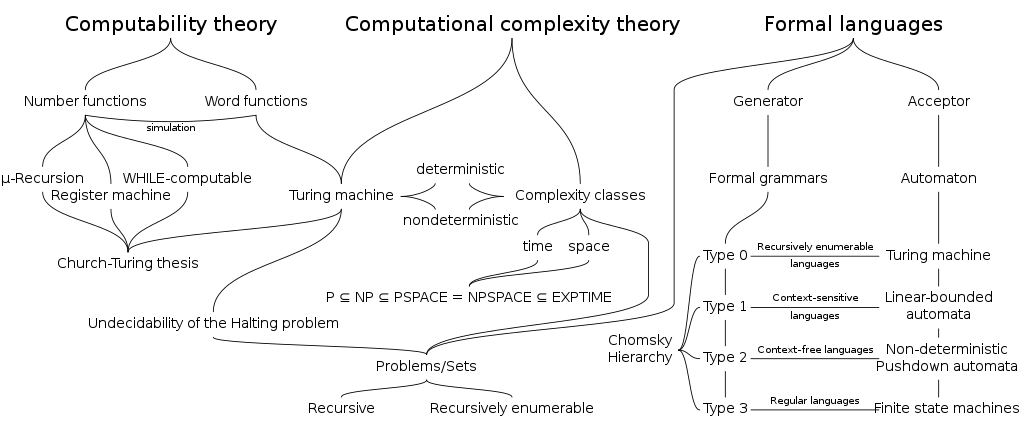
Formulazione della tesi di Church-Turing
La Tesi di Church-Turing è una proposizione ipotetica nella teoria della calcolabilità che suggerisce che qualsiasi funzione matematicamente calcolabile può essere calcolata da una macchina di Turing universale o da un equivalente formalmente equivalente, come il concetto di algoritmo esprimibile con le nozioni di algoritmo descritte dalla macchina di Turing.
Alonso Church – By Princeton University, Fair use, https://en.wikipedia.org/w/index.php?curid=6082269
In altre parole, la Tesi di Church-Turing afferma che se un certo processo può essere descritto in modo algoritmico (ovvero può essere “calcolato” in senso matematico), allora può essere modellato e simulato da una macchina di Turing. Questo è un principio fondamentale nella teoria dell’informatica che collega diverse nozioni di calcolabilità, come i calcolatori, le funzioni matematiche e i concetti di calcolo.
La Tesi di Church-Turing non è stata dimostrata, ma è piuttosto un’ipotesi che è stata ampiamente accettata sulla base delle prove empiriche che mostrano la capacità delle macchine di Turing e dei modelli equivalenti di esprimere una vasta gamma di processi algoritmici. La tesina ha contribuito a stabilire l’idea di calcolabilità e ha fornito la base per lo sviluppo della teoria dell’informazione e della computazione. Se un linguaggio di programmazione è in grado di esprimere tutte le funzioni calcolabili (cioè, se può simulare il comportamento di una macchina di Turing universale), allora è possibile affermare che quel linguaggio è “computazionalmente completo”.
Questa applicazione aiuta a stabilire i limiti e le capacità di vari linguaggi di programmazione e consente agli sviluppatori di comprendere quali problemi possono essere risolti utilizzando un determinato linguaggio. Ad esempio, la costruzione di linguaggi di programmazione con caratteristiche avanzate o paradigmi specifici può essere guidata dalla comprensione di come tali linguaggi possono simulare le macchine di Turing o altri modelli equivalenti.
Alan Turing – By Possibly Arthur Reginald Chaffin (1893-1954) – http://www.turingarchive.org/viewer/?id=521&title=4, Public Domain, https://commons.wikimedia.org/w/index.php?curid=22828488
Inoltre, la Tesi di Church-Turing è alla base della teoria dell’automazione e dell’informatica teorica. Essa aiuta a definire ciò che può essere calcolato e a stabilire i limiti delle capacità di calcolo. Pertanto, l’applicazione principale della Tesi di Church-Turing è nell’orientare la progettazione dei linguaggi di programmazione, la comprensione della calcolabilità e la definizione dei concetti fondamentali nella teoria dell’informazione e della computazione.
Tutorial, approfondimenti tematici e notizie in ambito tecnologico. Credits immagini: pexels.com, pixabay.com, wikipedia.org se non diversamente specificato. Questo articolo non contiene necessariamente suggerimenti, pareri o endorsement diretti da parte del proprietario del progetto. Per contatti clicca qui
